| Using the Titanic to Teach Archimedes Principle |
|---|
| Posted on Thu 21 Dec 2006 (131291 reads) |
|
By Peter J. Yonko One line in a scene from the movie Titanic was the inspiration for one of my physics lessons. Watching this scene, I saw how I could use the mystique of the great ship to bring Archimedes principle to life. In the scene, we see Mr. Andrews, Titanic's designer, enter with several ship drawings. He unfolds them on a table with great urgency. As Andrews explains the dire situation, Captain Smith asks eagerly about the pumps. Andrews replies, From this moment, no matter what I do, Titanic will founder. Mr. Ismay, an executive with White Star Lines, says in disbelief, But this ship can't sink! Andrews sternly replies, She is made of iron, sir. I assure you she can and she will. It is a mathematical certainty. Behind this statement lies the principle that explains why Titanic was able to float and why she could not remain afloat after striking the iceberg. A complete explanation of the principle behind Andrews statement would not be appropriate for a feature film; however, when studying fluids in a physics class, the story of the Titanic is perfect for teaching Archimedes principle: a body wholly or partially submerged in a fluid is buoyed up by a force equal to the weight of the displaced fluid. In the following months, as the film's popularity grew it had an audience of over 100 million people, many of them teenagers and knew that I had come across a valuable resource for teaching Archimedes principle in my high school physics classes. The producers of the film recreated Titanic with great detail. The audience was able to understand what was happening to the ship after she struck the iceberg because of the computer-generated images of her sinking. Mr. Andrews was certain of Titanic's demise because he knew Archimedes principle. With more than four compartments flooded, it was physically impossible for Titanic to stay afloat. The following drawings (not to scale) have been included to bring to mind how Titanic was structured, how the hull pushed away tons of water in order to buoy her up, and how Titanic broke apart in her final moments. Drawings like these could be included in a computer-aided presentation program (i.e., Corel Presentations 8 or Microsoft PowerPoint). In addition, showing the actual scene described in the first paragraph can further enhance the presentation. 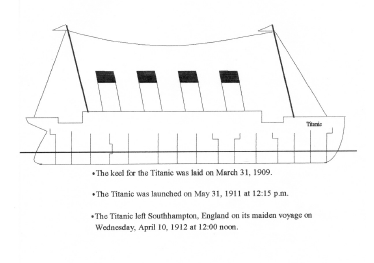 In order to relate the Titanic and Archimedes principle, some specific information about the Titanic must be known. First, the hull was designed to displace (push away) 66,000 tons of water. Its gross weight was 46,328 tons. Therefore, the Titanic had 19,672 tons (66,000 tons - 46,328 tons) of extra displacement capacity. If Titanic lost more than 19,672 tons of displacement capacity, her gross weight would exceed her buoyant force and she would sink. The hull was divided into 16 compartments separated by 15 watertight bulkheads. For my purposes in the classroom, I make what I believe to be a reasonable generalization: that each compartment of the hull has the same displacement capacity: 4125 tons (66,000 tons/16 compartments). 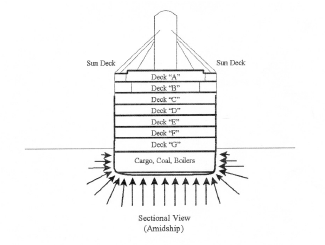 After explaining to the class the generalizations regarding the calculations, the class examines the loss of displacement capacity by compartment: One flooded compartment: 19,672 - 4,125 = 15,547. Titanic is able to stay afloat. Two flooded compartments: 19,672 - 8,250 = 11,422. Titanic is able to stay afloat. Three flooded compartments: 19,672 - 12,375 = 7,297. Titanic is able to stay afloat. Four flooded compartments: 19,672 - 16,500 = 3,172. Titanic is able to stay afloat. Five flooded compartments: 19,672 - 20,625 = -953. Titanic is not able to stay afloat. 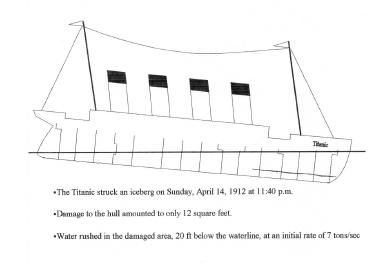 After discussing how Archimedes principle relates to the Titanic, the students make their own model boats to demonstrate the same principle. Simple boats can be made out of plastic containers or cardboard covered with masking tape. Students can create a crude hull (rectangular, triangular, or semicircular) out of these materials. Once the shape is decided upon, the next task is to calculate the volume of the hull. When the volume of the hull is known, the buoyant force can be calculated from Archimedes principle: Fb = rgV, where r is the density of the displaced fluid (1000 kg/m3 for fresh water), g is the acceleration due to due to gravity (9.81 m/s2), and V is the volume of the hull. If the upward buoyant force is exceeded by the downward weight of any load placed in the boat, the boat will sink. Students can predict the maximum number of paper clips or pennies their boats can carry. My students gather around a small fish tank full of water in my classroom. Anticipation builds as their boats sit lower in the water with the addition of each penny. As the waterline creeps to the top of the hull, the moment of truth arrives. Students rejoice if they drop in the last penny and the boats stays afloat or they despair as their boat sinks to the bottom of the tank. I am continually amazed how often everyday experiences can develop into valuable classroom material. Driving to work in the morning at increasing velocity, decreasing velocity, and rounding a curve kindles a lesson on acceleration. A walk along the beach contemplating the tides can lead to a classroom discussion on the gravitational attraction between masses, the moon and the oceans. During a hike in the woods, a demonstration of the surface tension of water might be inspired by the sight of water striders skimming across the surface of a still pool in a dried-up streambed. In my case, the silver screen was the source of an interesting way to explain a physics concept. Observant teachers can find inspiration for their classrooms if they think of the world as a stage where physical wonders are showcased twenty-four hours a day. Many thanks go to By Peter J. Yonko for this contribution. |
| Index :: Print :: E-mail |
The comments are owned by the poster. We aren't responsible for their content.












































